или больше типов связей, то спайность развивается поперек наиболее слабых связей; мягкость и совершенная спайность графита, химически идентичного алмазу, обусловлены слабостью остаточных связей между слоями атомов углерода, внутри же этих слоев связи прочные и тесные.

Оптические свойства также связаны со структурой. Показатель преломления алмаза и сфалерита высок вследствие гомеопо-лярного характера всех действующих в них связей. Структура определяет симметрию оптических свойств; например, присутствие в структуре параллельных плоских групп атомов (листоватость) приводит, как правило, к резкой анизотропии, когда оптические и другие физические свойства сильно меняются в кристалле в зависимости от направления.

Отражение, преломление и дисперсия света.

Поскольку камень, пригодный для целей украшения, должен привлекать к себе взгляды, наиболее важны с этой точки зрения его оптические свойства. В самом деле, все искусство огранки драгоценных камней состоит в том, чтобы придать камню такую форму, при которой наилучшим образом проявятся именно эти свойства. Чтобы понять, почему камням придается определенная огранка, важно установить, что происходит с лучом света, попадающим на поверхность камня. При этом мы обнаружим, что действие камня на луч света приводит к результатам, играющим важную роль в отделении одних видов драгоценных камней, особенно граненых, от других.

Поведение светового луча, наталкивающегося на поверхность, разделяющую какие-либо две среды, одинаково вне зависимости от природы этих сред. Повседневный опыт обращения с зеркалом показывает, что луч света возвращается, или, как обычно говорят, отражается от плоской и гладкой поверхности, причем кажущиеся размеры предметов, наблюдаемых в отраженном виде, не меняются, не. правая и левая стороны меняются местами; говорят, что предмет и его зеркальное отображение энантиоморфны. Если.

использовать второе плоское зеркало и наблюдать в нем отражение от первого аеркала, то второе отражение не отличается от вредмета, хотя мы и не можем разместить глаза на втором отражении на одной линии со своими собственными. Мы видим, что наше отражение в плоском зеркале кажется расположенным как

раз на таком расстоянии позади этого зеркала, на каком мы находимся перед ним. .

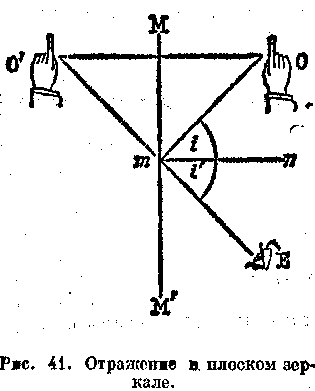
На рис. 41 линия ММ показывает профиль плоского зеркала, О’ — отражение в зеркале руки О. Луч от О попадает в глаз Е от точки т на поверхности зеркала, но кажется, что этот луч идет от О. Поскольку линия 00 перпендикулярна зеркалу, а точки О -а О одинаково удалены от него, из элементарной геометрии следует, что угол г, образуемый отраженным лучом с линией тп, нормальной к зеркалу, равен углу i между падающим лучом и той же линией.

Кроме того, повседневный опыт учит нас, что дело обстоит не так просто, если луч света пересекает поверхность, разделяющую две среды, и переходит из первой среды во вторую. Так, если мы посмотрим в бассейн с водой, то дно бассейна покажется нам ближе, чем на самом деле, а если мы погрузим в воду под некоторым углом палку, то она покажется нам согнутой у поверхности воды. Поскольку сама палка при этом не сгибается, асщ, что направление светового луча испытывает какое-то изменение, когда он входит в воду и выходит из нее. Прохождение.

луча света из одной среды в другую изучал в начале XVI в. Снел-лиус

. Он вывел следующие законы преломления света:.

1.

Преломленный луч лежит в плоскости, содержащей падающий луч и нормаль к плоской поверхности, разделяющей две среды. (Заметим, что этот закон справедлив и для отраженного луча.).

2.

Угол г, образуемый преломленным лучом с нормалью, связан с углом г, образуемым падающим лучом с тем же направлением, следующим уравнением:

где га и re — константы двух сред, называемые показателями преломления.

Приведенное простое тригонометрическое соотношение можно выразить геометрически. Предположим, что мы рассматриваем плоское сечение SOS (рис. 42), которое располагается под прямым углом к поверхности, разделяющей две среды, и содержит падающий луч10. Согласно первому закону Снеллиуса, преломленный луч OR также находится в этой плоскости. Проведем нормаль и опишем из центра О окружность произвольного радиуса, которая пересечет падающий луч в точке ц, а преломленный — в точке Ъ; опустим из этих точек перпендикуляры аа нор

маль NON : ас ж bd. Тогда мы получим: п-ас=п •Ьа, откуда видно, что при п>п ас

< bd и, следовательно, когда луч проходит из одной среды в другую, оптически менее плотную, он изгибается,.

т. е, преломляется, переходя через границу, и удаляется от нормали.

В дальнейшем мы увидим, что для того, чтобы понять сложность прохождения света в двупреломляющем кристалле, лучше всего вспомнить, что свет представляет собой волновое движение, и к этому простому случаю прохождения света из одной среды в другую вполне уместно применить волновую теорию. На рис. 43 показано сечение SOOS, располагающееся под прямым углом к плоскости, разделяющей две среды; JO, 1’0 — падающая волна, OR, OR — преломленная волна; ОР и ОР, проведенные перпендикулярно ГО и OR соответственно, показывают положение волнового фронта, когда он достигает границы в точке О и покидает первую среду в точке О’. Если, как и раньше, нижняя среда на рис. 43 оптически более плотная, скорость v световой волны в этой среде меньше, чем скорость v в другой среде (эта скорость обратно пропорциональна показателю преломления), и поэтому отрезок РО, пропорциональный v, меньше отрезка ОРпропорционального v. Углы РОО и Р00 — это углы i и г, т. е. угол падения и угол преломления. Поскольку 00 — общая сторона двух треугольников — РОО и РОО, а углы при вершинах Р и Р — прямые, мы имеем: v/sin i=v/sin г, или, что то же самое, nsini=resinr.

Когда свет падает на поверхность между двумя средами описанным выше образом, часть световых лучей, как было показано, преломляется, проходя во вторую среду; необходимо отметить, однако, что по крайней мере часть их отражается и остается в первой среде, а при определенных обстоятельствах, кан мы вскоре увидим, свет вообще не попадает во вторую среду. Отношение между количествами отраженного и преломленного света тесно связано с величиной угла падения и показателями преломления двух сред. Мы вернемся к этому вопросу, когда будем рассматривать вопрос о блеске камней.

Обратимся теперь к пути лучей при различных угла! падения, когда свет проходит из одной среды в другую, например из воды.

в, воздух. В случае малого угла падения, как у луча 1

О (рис. 44), часть лучей отражается в направлении 01[ и остается в первой среде, а остальные преломляются в направлении OR

и уходят во вторую среду. Такая же картина наблюдается и для луча I/): часть света отражается вдоль линии ОГ

, а остальные преломляются и идут по линии OR

. Поскольку в данном случае свет переходит в среду оптически менее плотную, т. е. имеющую более низкий показатель преломления, угол преломления будет больше угла падения. Следовательно, определенному лучу 1

О соответствует преломленный луч, скользящий вдоль граничной плоскости. Для лучей, таких, как 1

0, имеющих большой угол падения, соответствующих лучей во второй среде уже нет, или, иными ело-.

вами, луч Полностью отражается в более плотной среде. Предельный угол l

ON, называемый углом полного внутреннего отражения, связан очень простой зависимостью с показателями преломления двух сред; поскольку угол г в этом случае прямой, то sin г=1, и уравнение (1) принимает вид

Следовательно, если измерен угол полного внутреннего отражения и известен один из показателей преломления* то другой можно легко рассчитать.

Явление полного внутреннего отражения можно хорошо понять, если держать над головой стакан воды и смотреть на свет

лампы, стоящей, скажем, на столе и отражающейся от поверхности воды снизу. Это отражение будет несравнимо более ярким, чем то, каро^ можно получить при отражении от воды сверху.

Показатель преломления воздуха принят равНым единице; строго говоря, таков показатель преломления для вакуума, но различие настолько мало, что ОнО не может повлиять на точность даже очень тонких определений. Показатели преломления всех веществ меняется в зависимости от цвета, т. е. от длины световой волны, поэтому обычно в качестве стандарта используется желтый свет, испускаемый пламенем натрияк этому цвету наши.

глаза наиболее чувствительны. Если имеется подходящее электрическое оборудование, то яркий желтый свет можно получить от натровой лампы; желтое пламя можно также получить путем испарения крупинки соды или соли в пламени лабораторной газовой горелки (горелки Бунзена).

: Беглый взгляд на список показателей преломления драгоцен-вд камней, приведенный в части IV, показывает, что измерение этих показателей служит мощным средством определения того,

к какому виду относится данный граненый камень. Как лучше всего выполнить это измерение, рассказывается в следующей главе. Хотя показатель преломления считается физической константой, он может меняться в весьма широких пределах для разных образцов одного и того же минерального вида благодаря широте химического состава, обусловленной изоморфным замещением одного элемента другим без существенного изменения кристаллической структуры. Некоторые колебания показателя преломления можно обнаружить даже в одном и том же камне при измерениях в разных направлениях; это происходит вследствие замечательного свойства, которым обладают все кристаллические вещества, не относящиеся к высшей (кубической) сингонии,— свойства расщеплять падающий луч света на два луча. Это явление двойного лучепреломления, или двупреломления, обсуждается в одной из последующих глав.

С различной величиной показателя преломления вещества для света разного цвета связаны такие знакомые явления, как радуга.

и сияние алмаза. Когда дневной свет попадает внутрь камня, он становится не белым, а разлагается в спектр. За исключением ряда аномальных веществ, которых, кстати, нет среди драгоценных камней, показатель преломления последовательно возрастает при уменьшении длины световой волны, вследствие чего в обычном спектре один конец фиолетовый; дальше идут цвета синий, зеленый, желтый, оранжевый и на другом конце — красный. Угловая ширина спектра, которую можно измерить по разности показателей преломления для крайних частей спектра — фиолетовой и красной, также различная, хотя в целом она возрастает с увеличением показателя преломления. Это как раз ja дисперсия света, которая вызывает сияние, световую игру — важнейшее свойство бесцветных прозрачных драгоценных камней, без которого эти камни не привлекали бы такого внимания. В этом отношении алмаз превосходит все природные бесцветные камни, хотя к нему близок циркон, окраска которого исчезает при нагревании; однако еще сильнее дисперсия света в почти бесцветном искусственном рутиле, сиптетическом титанате стронция и в трех окрашенных минералах: демайтоиде (зеленом гранате), сфене и сильнее всего в касситерите.

Величины дисперсии света для важнейших драгоценных камней приведены в части IV. В качестве стандарта в этой книге использованы линии В (6870 А) и G (4308 А), расположенные вблизи красного и фиолетового концов видимой части спектра соответственно, но в таблице добавлены величины дисперсии для более узкого интервала: от С (6563 А) до F (4861 А), применяемого в случае оптических стекол; тем самым облегчается сравнение стекол и драгоценных камней по относительной дисперсии. Необходимо отметить, что для точного определения дисперсии света в каком-либо камне следует использовать монохроматический свет с длиной волны, максимально близкой к границам выбранного интервала: либо В и G, либо С и F. Если составить диаграмму зависимости показателя преломления минерала от длины световой волны, то в результате получится не прямая линия (даже приблизительно), а линия переменной кривизны, что можно видеть на примере алмаза (рис. 45). Величины дисперсии имеет смысл сравнивать между собой только в интервале идентичных длин волн.