Для целей описания положение каждой грани на поверхности кристалла приводится к системе трех прямых линий, пересекающихся в начале координат, так же как это делается в геометрии. Эти прямые линии называются кристаллографическими осями. До того как стало возможным изучать внутреннюю структуру кристаллов непосредственно, с помощью рентгеновских лучей, положение этих осей определялось по внешней морфологии. Проще всего эти оси можно себе представить в объемных «единичных ячейках», из которых, как теперь известно, и построены все кристаллы (рис. 32).
В кубической сингонии кристаллографические оси — это. система трех равных отрезков а*, а
, а
, параллельных ребрам единичного куба и расположенных под прямыми углами. В тетрагональной сингонии элементарная ячейка — прямая призма квадратного сечения; кристаллографические оси опять располагаются под прямыми углами, но вертикальная ось с (параллельная четверной оси симметрии) отличается по длине от одинаковых горизонтальных отрезков aj, а
. Осевое отношение с/а определяется как отношение длин сторон элементарной ячейки; так, v циркона
В ромбической сингонии элементарная ячейка — это прямоугольный параллелепипед с разными по величине отрезками а, Ь, с, параллельными трем двойным осям симметрии и также расположенными под прямыми углами. У топаза а=4,650, 6=8,800, с=8,394, осевое отношение а/b : 1 s c/b равно 0,528 s 1 i 0,954.
В моноклинных кристаллах структура такова, что выбрать элементарную ячейку, в которой оси располагаются под прямыми углами, уже нельзя. Ячейка здесь представляет собой наклонную призму, условно помещаемую так, чтобы ось а оказалась наклоненной в сторону наблюдателя вниз, образуя в плоскости симметрии угол Р>90° с вертикальной осью с; кристаллографическая ось Ъ параллельна двойной оси симметрии и, следовательно, перпендикулярна плоскости, содержащей оси а и с. У диопсида а ~ =9,73, 6=8,91, с=5,25, р = 105°50, а у сфена а=6,56, Ь—8,72, с=7,44, р = 119°43.
В кристаллах, относящихся к триклинной сингонии, осей, идущих под прямыми углами, нет и кристаллографические оси располагаются неправильно; три неравные оси а, Ь, с наклонены ДРУГ к другу под углами а, (5, у, ни один из которых не равен 90°. Кристаллографические параметры аксинита: а=7,15, Ь= =9,16, с=9,86, а=88°4 р=81°36,
у=77
42.
В гексагональной и тригональной сингониях оказалось удобным использовать систему четырех кристаллографических осей:
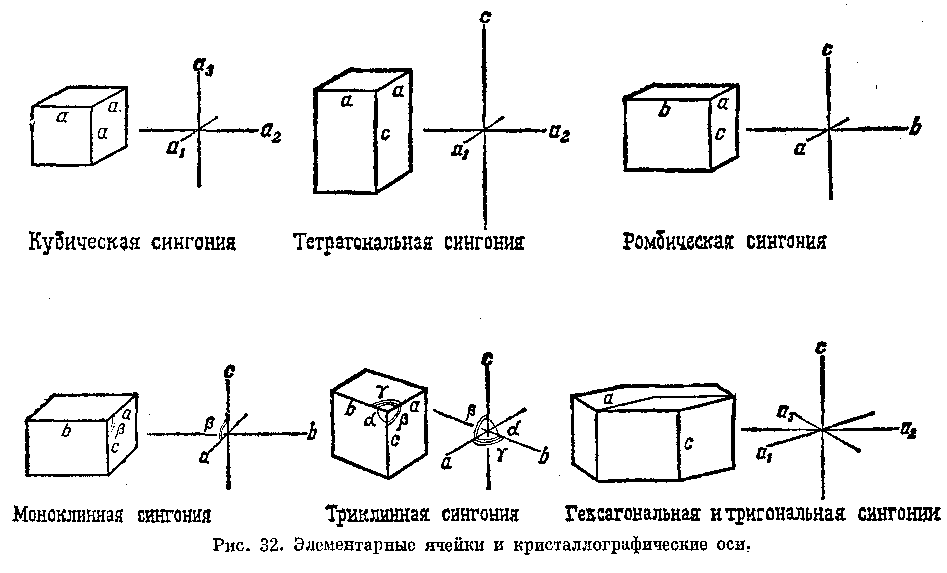
трех горизонтальных осей а±, а
, а
, расположенных под углами 120° друг к другу, и вертикальной оси с, перпендикулярной плоскости, содержащей первые три оси (следовательно, ось с параллельна шестерной или тройной оси симметрии).
Для обозначения взаимного расположения граней по отношений к кристаллографическим осям используется система индексов граней, или символов Миллера
(по фамилии Уильяма Хэл-лоуза Миллера, 1801—1880). Плоскость, отсекающая от кристаллографических осей отрезки, соотносящиеся между собой как ребра элементарной ячейки а, Ь, с, называется единичной плоскостью. Если эти ребра одинаковы, то индекс записывается 111 (читается: «один — один — один»). Индекс любой другой грани кристалла записывается (hkl), где alh, Ык, ell — отрезки, отсекаемые этой гранью на трех осях (рис. 33).
Таким образом, чтобы определить индекс какой-либо грани, надо разделить параметрические отрезки на отрезки, отсекаемые этой гранью, сокращая, если требуется, дроби. Мы упомянули выше, что у топаза а : Ъ : с=0,528 : 1 : 0,954; обнаружено, что две другие часто встречающиеся грани наклонены так, что они отсекают отрезки с осевыми отношениями 0,528 : 1 : 0,477 и оо : 1 : 1,918. Следовательно, индексы этих граней будут следующими:
Тот факт, что в кристаллах всех симметрий существуют такие простые соотношения, позволил сформулировать запоя рациональности индексов (индексы граней можно выразить небольшими
целыми числами или нулем). Из этого закона следуют важные выводы, касающиеся характера внутренней структуры кристаллов; эти выводы полностью подтвердились затем при рентгеноскопии кристаллов.
Отрезок, отсекаемый на отрицательном продолжении оси, обозначается чертой над соответствующей цифрой; так, индекс передней нижней правой грани октаэдра (рис. 34) — (111) (читается: «один — один — минус один»). Цифра 0 в индексе, обозначающая отсекаемый отрезок бесконечной длины, соответствует параллельному расположению грани относительно данной оси; куб, например, состоит из шести граней: (100), (010), (001) (100), (ОТО), (001). Совокупность всех граней, образующих ту или иную ферму, обозначается индексом одной из этих граней: например, куб — эт» форма {100} кубической сингонии, октаэдр — форма {111}.
Индексы для тригональных и гексагональных кристаллов, для котвры$ используется система четырех кристаллографических всей, состоят аз четырех цифр; третья цифра не является, конеч-.
но, независимой: величина отрезка, отсекаемого на третьей горизонтальной оси, определяется отрезками по двум другим осям, и в результате сумма первых трех цифр в таких индексах всегда равна нулю. Единичными плоскостями в этой записи можно считать плоскости (1011) или (1121).